Sin 120
In Mathematics, trigonometry is a branch that deals with the study of measures of right-angle triangles such as length, height and angles. Trigonometry has enormous applications in various fields, such as Architecture, Navigation systems, sound waves detections, and so on. In this article, let us discuss the value of sin 120, and the various methods which are used to find the sin 120 values using other trigonometric angles and identities are explained in detail. Also, go through the below-provided article to learn all the sine values.
How to Derive the Value of Sin 120 Degrees?
The sin 120-degrees value can be identified using either unit circle or with the help of other trigonometric angles such as 60, 180 degrees and so on. Let us consider the value 120 degrees in the cartesian plane. We know that the cartesian plane is divided into four quadrants. The value 120 degrees falls on the second quadrant. As the value of sine function in the second quadrant takes the positive value, the value of sin 120 degrees should be a positive value.
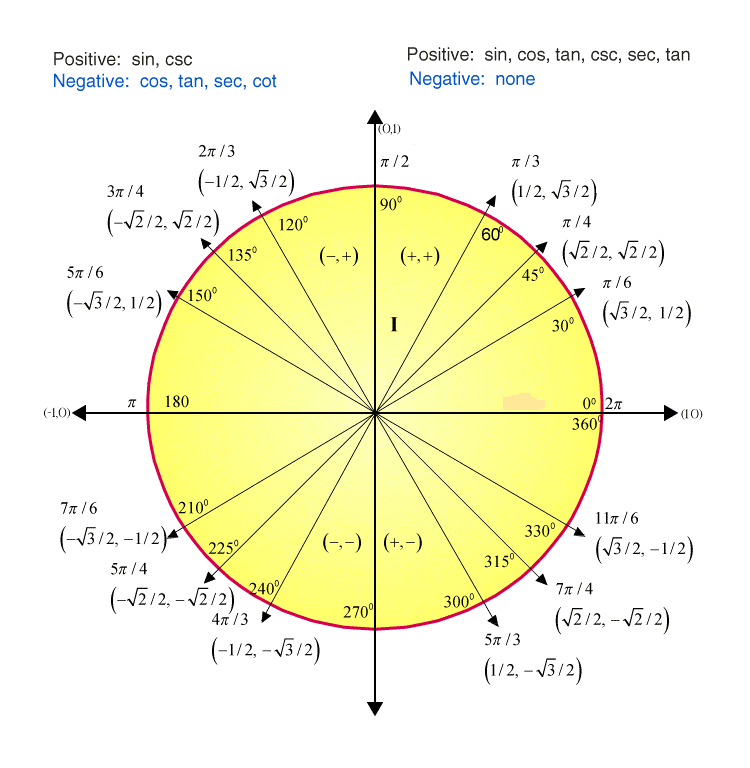
By using the unit circle, the value of sin 120 can be calculated. We know the radius of the circle is the hypotenuse of the right triangle which is equal to the value 1. From the cartesian plane, we take, x= cos and y = sin
By looking at the diagram given above, the value of sin 60 is equal to the value of sin 120.
It means that, sin 60 = sin 120 = √3/2.
Method 1
Another method to find the value of sin 120 degrees is by using the other angles of the sine functions such as 60 degrees and 180 degrees which are taken from the trigonometry table.
We know that
180° – 60° = 120°
Also, we know that the trigonometric identity sin (180°- a ) = sin a
Now,
Sin ( 180°- 120°) = sin 120°
Therefore, sin 120°= sin 60°
From the trigonometry table, use the value of sin 60° which is equal to √3/2.
Hence, the value of sin 120 degrees is √3/2
Method 2
By using the value of cosine function relations, we can easily find the value of sin 120 degrees.
Using the trigonometry formula, sin (90 + a) = cos a, we can find the sin 120 value.
As given, sin (90° +30°) = cos 30°
It means that sin 120° = cos 30°
We know that the value of cos 30 degrees is √3/2.
Therefore, sin 120° = √3/2.
Here, the values of other important trigonometric angles for different ratios are provided here for the reference.
|
Trigonometry Ratio Table |
||||||||
|
Angles (In Degrees) |
0 |
30 |
45 |
60 |
90 |
180 |
270 |
360 |
|
Angles (In Radians) |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
π |
3π/2 |
2π |
|
sin |
0 |
1/2 |
1/√2 |
√3/2 |
1 |
0 |
−1 |
0 |
|
cos |
1 |
√3/2 |
1/√2 |
1/2 |
0 |
−1 |
0 |
1 |
|
tan |
0 |
1/√3 |
1 |
√3 |
Not Defined |
0 |
Not Defined |
1 |
|
cot |
Not Defined |
√3 |
1 |
1/√3 |
0 |
Not Defined |
0 |
Not Defined |
|
cosec/csc |
Not Defined |
2 |
√2 |
2/√3 |
1 |
Not Defined |
−1 |
Not Defined |
|
sec |
1 |
2/√3 |
√2 |
2/√3 |
Not Defined |
−1 |
Not Defined |
1 |
Register with BYJU’S – The Learning App and download the app to get all the Maths-related articles and learn in an easy way.