Sin 45 Degrees
In trigonometry, there are three primary ratios, Sine, Cosine and Tangent, which are used to find the angles and length of the right-angled triangle. Before discussing Sin 45 degrees, let us know the importance of Sine function in trigonometry. Sine function defines a relation between the acute angle of a right-angled triangle and the opposite side to the angle and hypotenuse. Or you can say, the Sine of angle α is equal to the ratio of the opposite side(perpendicular) and hypotenuse of a right-angled triangle.
The trigonometry ratios sine, cosine and tangent for an angle α are the primary functions. The value for sin 45 degrees and other trigonometry ratios for all the degrees 0°, 30°, 60°, 90°,180° are generally used in trigonometry equations. These values are easy to remember with the help trigonometry table, which will also be provided in this article.
Let us discuss first discuss sin 45 degrees value, here in this article.
Sin 45 Degree Value
Let us consider a right-angled triangle △ABC. Thus, the sine of angle α is a ratio of the length of the opposite side,BC to the angle α and its hypotenuse AB.
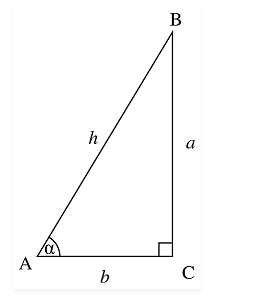
Sin α = \(\frac{Opposite Side}{Hypotenuse}\)
= \(\frac{Perpendicular}{Hypotenuse}\)
= BC/AB
So, sin 45 degrees trigonometry value, in-fraction will be, sin 45° = \(\frac{Perpendicular}{Hypotenuse}\)
A simple method by means of which we can calculate the value of sine ratios for all the degrees is discussed here. After learning this method, you can easily calculate the values for all other trigonometry ratios. So, let’s start to calculate the value for sin 45 degrees table of trigonometry.
Sin 0°= \(\sqrt{0/4}\) = 0
Sin 30° = \(\sqrt{1/4}\) = ½
Sin 45° = \(\sqrt{2/4}\) = \(1/\sqrt{2}\)
Sin 60°= \(\sqrt{3/4}\) = \(\sqrt{3}/2\)
Sin 90° = \(\sqrt{4/4}\) = 1
Therefore, Sine ratio table for both degrees and radians can be written as;
| Sine 0° | 0 |
| Sine 30° or Sine π/6 | 1/2 |
| Sine 45° or Sine π/4 | \(1/\sqrt{2}\) |
| Sine 60°or Sine π/3 | \(\sqrt{3}/2\) |
| Sine 90° or Sine π/2 | 1 |
| Sine 120° or Sine 2π/3 | \(\sqrt{3}/2\) |
| Sine 150° or Sine 5π/6 | 1/2 |
| Sine 180° or Sine π | 0 |
| Sine 270° or Sine 3π/2 | -1 |
| Sine 360°or Sine 2π | 0 |
In the same way, we can find the values for other trigonometry ratios such as cosine and tangent. Here we are providing you the table for sine, cosine and tangent ratios.
| Degrees | 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
| Sin | 0 | 1/2 | \(1/\sqrt{2}\) | \(\sqrt{3}/2\) | 1 | 0 | -1 | 0 |
| Cos | 1 | \(\sqrt{3}/2\) | \(1/\sqrt{2}\) | 1/2 | 0 | -1 | 0 | 1 |
| Tan | 0 | 1/\(\sqrt{3}\) | 1 | \(\sqrt{3}\) | ∞ | 0 | ∞ | 0 |
Learn more about trigonometric ratios and formulas and identities and download BYJU’S-The Learning App for a better experience.
| Related Links | |
| Sin 0 Degree | Sin 30 Degrees |
| Sin 60 Degrees | Sin 90 Degrees |