Square Root Numbers
The square root numbers are the list of those numbers, which produce the original numbers when multiplied by themselves. The symbol used to represent the square root is a radical sign, i.e. ‘√’. The number present under the radical symbol is called ‘radicand’. This concept is one of the important concepts for Class 9 students.
To learn about square roots, we should first learn about squares of numbers. Then it will be easy for us to find the square roots of the numbers. When we multiply a number by itself, then it is said to be the square of that number. Suppose ‘a’ is a number and is multiplied by itself, then it is said to be squared. For example, 2 x 2 = 22 = 4. If we find the square root of 4, we get the original number, i.e. 2, since 4 is a perfect square. Therefore, it can be easily factored by the prime factorisation method to get the square root. See some more examples below:
- 3 squared = 32 = 9 & √9 = 3
- 7 squared = 72 = 49 & √49 = 7
- 11 squared = 112 = 121 & √121 = 11
- 12 squared = 122 = 144 & √144 = 12
How To Find a Square Root of Numbers?
There are different methods to find the square root of given numbers. They are explained below along with an example in each case.
Method 1: Repeated Subtraction Method
The easiest and a simple method to find the square root of a given number is repeated subtraction. In this method, we need to subtract the consecutive odd numbers till we get 0. However, this method is suitable for only perfect square numbers, such as 4, 9, 16, 25, etc. Let us find the square root of 81 using this method.
81 – 1 = 80
80 – 3 = 77
77 – 5 = 72
72 – 7 = 65
65 – 9 = 56
56 – 11 = 45
45 – 13 = 32
32 – 15 = 17
17 – 17 = 0
Here, we subtracted 9 consecutive odd numbers. So, the square root of 81 is 9.
Method 2: Prime Factorisation Method
In this method, we need to express the given number as the product of its prime factors. This method is also applicable for perfect squares. Let’s look at the example given below to understand how to find the square root of a number using prime factorisation.
Example:
Consider the number 225.
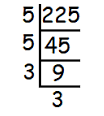
The product of prime factors of 225 is:
225 = 3 × 3 × 5 × 5
Take the square root on both sides.
√225 = √(3 × 3 × 5 × 5)
= √(32 × 52)
= 3 × 5
= 15
Thus, the square root of 225 is 15.
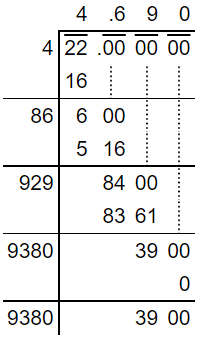
Method 3: Long Division Method
Finding the square root of very large numbers or imperfect squares could be a difficult task. Hence, we use the long division method to find the square root of such numbers in an easy and fastest way.
Let us find the square root of 10 using this method.
√10 = 3.162…
Therefore, the square root of 10 upto 3 decimal places is 3.162.
Square Root Numbers List
Here is the list of the square of numbers and their square roots. The table given below can be memorised by students easily so that they can solve questions based on these square root values.
| Number (n) | Square (n2) | Square root (√n) |
| 1 | 1 | 1 |
| 2 | 4 | 1.4142 |
| 3 | 9 | 1.7321 |
| 4 | 16 | 2 |
| 5 | 25 | 2.2361 |
| 6 | 36 | 2.4495 |
| 7 | 49 | 2.6458 |
| 8 | 64 | 2.8284 |
| 9 | 81 | 3 |
| 10 | 100 | 3.1623 |
| 11 | 121 | 3.3166 |
| 12 | 144 | 3.4641 |
| 13 | 169 | 3.6056 |
| 14 | 196 | 3.7417 |
| 15 | 225 | 3.8730 |
| 16 | 256 | 4 |
| 17 | 289 | 4.1231 |
| 18 | 324 | 4.2426 |
| 19 | 361 | 4.3589 |
| 20 | 400 | 4.4721 |
| 21 | 441 | 4.5826 |
| 22 | 484 | 4.6904 |
| 23 | 529 | 4.7958 |
| 24 | 576 | 4.8990 |
| 25 | 625 | 5 |
| 26 | 676 | 5.0990 |
| 27 | 729 | 5.1962 |
| 28 | 784 | 5.2915 |
| 29 | 841 | 5.3852 |
| 30 | 900 | 5.4772 |
| 31 | 961 | 5.5678 |
| 32 | 1024 | 5.6569 |
| 33 | 1089 | 5.7446 |
| 34 | 1156 | 5.8310 |
| 35 | 1225 | 5.9161 |
| 36 | 1296 | 6 |
| 37 | 1369 | 6.0828 |
| 38 | 1444 | 6.1644 |
| 39 | 1521 | 6.2450 |
| 40 | 1600 | 6.3246 |
| 41 | 1681 | 6.4031 |
| 42 | 1764 | 6.4807 |
| 43 | 1849 | 6.5574 |
| 44 | 1936 | 6.6332 |
| 45 | 2025 | 6.7082 |
| 46 | 2116 | 6.7823 |
| 47 | 2209 | 6.8557 |
| 48 | 2304 | 6.9282 |
| 49 | 2401 | 7 |
| 50 | 2500 | 7.0711 |
Solved Examples
Question 1:
Find the square root of 169 using the repeated subtraction method.
Solution:
Given number: 169
Let us subtract the consecutive odd numbers from 169 as shown below:
169 – 1 = 168
168 – 3 = 165
165 – 5 = 160
160 – 7 = 153
153 – 9 = 144
144 – 11 = 133
133 – 13 = 120
120 – 15 = 105
105 – 17 = 88
88 – 19 = 69
69 – 21 = 48
48 – 23 = 25
25 – 25 = 0
Here, 13 consecutive odd numbers are subtracted.
Therefore, the square root of 169 is 13.
Question 2:
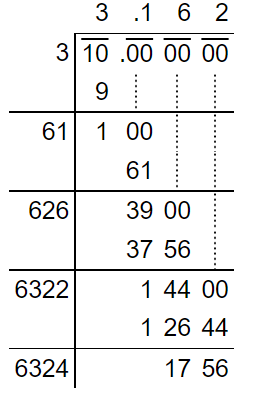
Find the square root of 22 using a suitable method.
Solution:
As 22 is not a perfect square number, we should apply the long division method.
√22 = 4.690…
Hence, the square root of 22 upto 3 decimal places is 4.690.
Square Root Problems
Based on the table above we can solve the questions given here.
- Solve √50 + √2 + √9
- Multiply: √3 and √7
- Divide: √49 by 7
- Simplify: (√8 x √9) + √89
- Simplify: 2√4+3√9+5√25
Related Articles
Video Lesson