The volume of a frustum of a cone depends on its slant height and radius of the upper and bottom circular part. Basically a frustum of a cone is formed when we cut a right-circular cone by a plane parallel to its base into two parts. Hence, this part of the cone has its surface area and volume.

Let us learn here to derive the volume of frustum and understand the concept better by solving the problems.

Derivation of Volume of Frustum of Cone

Let us consider a right circular cone which is cut by a plane parallel to its base as given in the below figure.

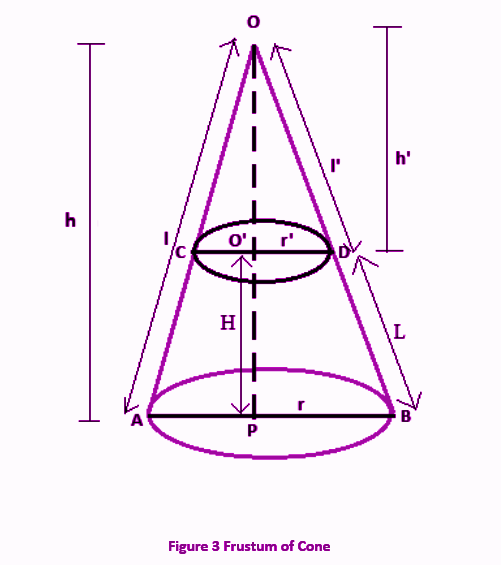
Here, we can consider the frustum as the difference between the two right circular cones.

Let,

Height of large cone = h

Slant height of large cone = l

and radius = r

Now,

Height of smaller cone = h’

Slant height of smaller cone = l’

And radius = r’

In case of frustum,

Height of frustum = H

Slant height= L

Now, we can say,

volume of bigger cone say V₁ = ⅓ π r²h

Also, volume of smaller cone, V₂ = ⅓ πr’²h’

Therefore,

Volume of frustum of cone, V = V₁ – V₂

V = ⅓ π r²h – ⅓ πr’²h’

V = ⅓ π (r²h – r’²h’) ……………(1)

From the figure, in the ∆OO’D and ∆OPB;

∠DOO’ = ∠BOP (Common Angle)

CD//AB (Plane cutting the cone is parallel to the base)

⇒∠O’DO = ∠PBO (Corresponding Angles)

Thus, ∆OO’D~∆OPD (By AA criterion of similarity)

As we know, by the condition of similarity, the ratio of sides of similar triangles are equal. Hence,

h’/h = r’/r …………………..(2)

Substituting the value of eq. 2 in eq. 1 we get;,

\(V\) = \(\frac{1}{3}~ π\left(r^2 \left(\frac{rh’}{r’}\right)~-~r’^2 h’\right)\) \(⇒~V\) = \(\frac{1}{3}~ πh’~ \left(\frac{r^3~-~r’^3}{r’}\right)\) …………(3)

From the figure we can see;

h = H + h′

Substituting this value in equation (2), we get;

\(\frac{h’}{H~+~h’}\) = \(\frac{r’}{r}\) \(⇒~\frac{h’}{H}\) = \(\frac{r’}{r~-~r’}\) \(⇒~h'\) = \(H\left(\frac{r’}{r~-~r’}\right)\)

Now putting the value of h’ in equation 3 we get;

\(V=\frac{1}{3}\pi H(\frac{r{‘}}{r-r{‘}})(\frac{r^3-r{‘}^3}{r{‘}})\) \(V=\frac{1}{3}\pi H(\frac{r-r{‘}}{r-r{‘}})({r^2+rr{‘}+r{‘}^2})\) \(⇒~V\) = \(\frac{1}{3}~ πH~(r^2~+~r’r~+~r’^2)\)

In few cases, we take,

r = R or r₁ and r’ = r or r₂

If radius of base of frustum is R and top of frustum is r, then the volume can be represented by:

Volume of frustum of cone = πh/3 (R²+r²+Rr)

If radius of base of frustum is r₁ and top of frustum is r₂ then the volume can be represented by:

Volume of frustum of cone = πh/3 (r₁²+r₂²+r₁r₂)

Slant Height of Frustum of Cone

The slant height of frustum of cone is determined by the formula:

Slant Height = √[(r₁ – r₂)² + h²]

The slant height of frustum plays an important role while determining its lateral surface area.

Problem and Solution

If the radius of base of cone is 20 m and radius of cone obtained after we have cut it by a plane is 8 m, and height of frustum of cone is 30 m, then find the volume of frustum.

Solution: Given,

R = 20 m

Base of small cone obtained will be the top of frustum.

Therefore, r = 8 m

Height of frustum = 30 m

By the formula of volume we know;

Volume of frustum of cone = πh/3 (R²+r²+Rr)

V = π(30)/3 (20²+8²+20×8)

V = 19611.42 cubic meter