An annulus is a shape made out of two circles. An annulus is a plane figure formed between two concentric circles (the circles sharing a common center). The shape of the annulus is like a ring. Some of the real-life examples of annulus shape are finger-ring, dough-nut, a CD, etc.  Let us learn its meaning in terms of geometry along with the area formula and solved examples based on it.

Annulus Definition

The region covered between two concentric circles is called the annulus. The concentric circles are the circles that have a common center. An annulus is a plane shape formed between these concentric circles. It looks like a circular path around the circle.

The circle is a fundamental concept not only in Maths but also in many fields. A circle is a plane figure that is made up of the points situated at the same distance from a particular point.

In the above figure, a circle with some radius is given.  Now if the same circle is surrounded by another circle with some space or gap in between them and the radius bigger than this circle, the region formed in between the two circles is basically the annulus.

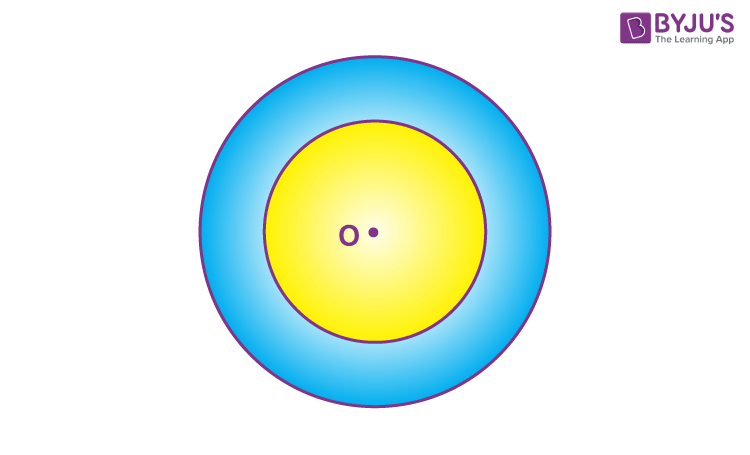
In the above figure, the blue shaded portion is the annulus.

Annulus Meaning

The word “annulus” (plural – annuli) is derived from the Latin word, which means “little ring“. An annulus is called the area between two concentric circles (circles whose centre coincide) lying in the same plane.

Annulus is the region bounded between two circles that share the same centre. This shape resembles a flat ring. It can also be considered as a circular disk having a circular hole in the middle. See the figure here showing an annulus.

Here, two circles can be seen, where a small circle lies inside the bigger one. The point O is the centre of both circles. The shaded coloured area, between the boundary of these two circles, is known as an annulus. The smaller circle is known as the inner circle, while the bigger circle is termed as the outer circle.

In other words, any two-dimensional flat ring-shaped object that is formed by two concentric circles is called an annulus.

Annulus Formula

Similar to other two-dimensional figures, the annulus also have two important formulas. They are:

• Area of annulus
• Perimeter of annulus

The area of the annulus can be determined if we know the area of circles (both inner and outer). The formula to find the annulus of the circle is given by:

A = π(R²-r²)

where ‘R’ is the radius of outer circle and ‘r’ is the radius of the inner circle.

Area of Annulus

The area of the annulus can be calculated by finding the area of the outer circle and the inner circle. Then we have to subtract the areas of both the circles to get the result. Let us consider a figure:

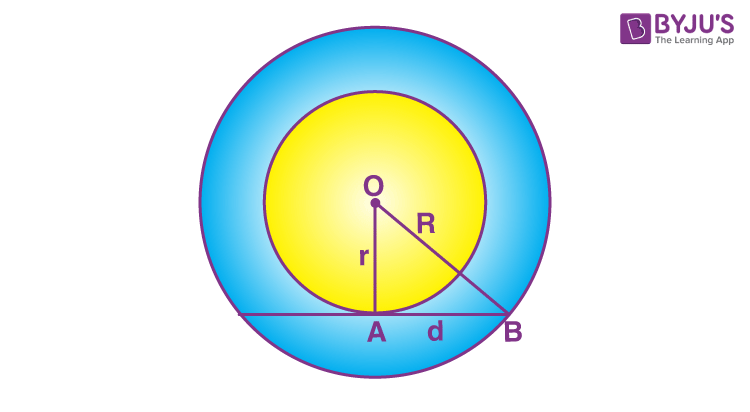
In the above figure, two circles are having common centre O. Let the radius of outer circle be “R” and the radius of inner circle be “r”. The shaded portion indicates an annulus. To find the area of this annulus, we are required to find the areas of the circles.

Therefore,

Area of Outer Circle = πR²

Area of Inner Circle = πr²

Area of Annulus = Area of Outer Circle – Area of Inner Circle

Hence,

Or we can also write it as;

Perimeter of Annulus

By the definition of the perimeter, we know it is the total linear distance covered by the boundaries of a two-dimensional shape. Hence, the perimeter of the annulus will be the total distance covered by its outer circle and inner circle.

Suppose the radius of outer circle is R and the radius of inner circle is ‘r’, then the perimeter of annulus will be:

Perimeter of annulus = 2πR + 2πr = 2π (R + r) units

The value of π is 22/7 or 3.14.

Related Articles

• Geometry
• Circles in Maths
• Concentric Circles
• Circumference
• 2D Shapes

Annulus Solved Examples

Q.1: Calculate the area of an annulus whose outer radius is 14 cm and inner radius 7 cm?

Solution: Given that outer radius R = 14 cm and inner radius r = 7 cm

Area of outer circle = πR² = 22/7 x 14 x 14

= 22 x 14 x 2

= 616 cm²

Area of inner circle = πr² = 22/7 x 7 x 7

= 22 x 7

= 154 cm²

Area of the annulus = Area of the outer circle – Area of the inner circle

Area of the annulus = 616 – 154

Area of the annulus = 462 cm²

Q.2: If the area of an annulus is 1092 inches and its width is 3 cm, then find the radii of the inner and outer circles.

Solution: Let the inner radius of an annulus be r and its outer radius be R.

Then width = R – r

3 = R – r

R = 3 + r

We know,

Area of the annulus = π(R²−r²)

or

Area of the annulus = π (R + r) (R – r)

1092 = 22/7 (3 + r + r) (3)

3 + 2r = 1092×722×3

3 + 2r = 115.82

2r = 115.82 – 3

2r = 112.82

r = 56.41

R = 3 + 56.41

= 59.41

So, Inner radius = 56.41 inches

Outer radius = 59.41 inches