The area of a square can be calculated using its diagonals. Apart from the traditional method of finding the area of a square by squaring the sides, this is one of the most useful methods to compute the area of a square if the diagonal length is given.

Formula to Calculate Area of a Square Using Diagonal

It is not always mandatory to have the measure of the side for computing a square’s area. If we have the length of the diagonal, then the area can be calculated as:

• Here, “d” is the length of any of the diagonal (in a square, diagonals are equal)

Derivation for Area of Square using Diagonal Formula

The formula to find the area of any square if its diagonals are given can be derived using Pythagoras theorem as explained below:

Consider a square of sides “a” units and diagonal as “d” units.

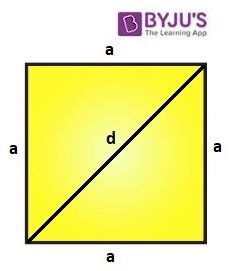
In the above figure, the square of the side “a” unit, has been divided into two right triangles with the help of diagonal of length “d” units. Thus, the diagonal of the square divides it into two right triangles. Consider any right triangle and apply Pythagoras theorem.

According to Pythagoras theorem, for a right-angled triangle,

Hypotenuse² = Perpendicular² + Base²

In the above diagram,

• Perpendicular = a
• Base = a
• Hypotenuse = d

So,

a² + a² = d²

⇒ 2a² = d²

Or, a² = d²/2

Now, area of a square = a² = d²/2

So, area of a square using diagonals = ½ × d² Square units.

Related Video Lesson

Example Question to Solve Area of Square When Diagonal is Given:

Question: Find the area of a square having a diagonal of length 10 cm.

Solution:

Given,

d = 10 cm

Now, the area of square = ½ × (diagonal)²

So,

A = ½ × 10²

Or, area = 50 cm²

Note: Using the diagonal, the perimeter of the square can also be found as explained below.

Finding Perimeter of Square Using Diagonal

It is known that the area of a square in terms of diagonal = ½ × d²

Now, a × a = ½ × d²

Or, a = √(½ × d²)

As the perimeter of square = 4a,

P = 4 × √(d²/2) units.

More Topics Related to Squares: