In conic sections, a conic having its eccentricity less than 1 is called an ellipse. i.e, the locus of points whose distances from a fixed point and straight line are in constant ratio ‘e’ which is less than 1, is called an ellipse. The fixed point and fixed straight line are called focus and directrix respectively. An ellipse has two points which are the focus of the ellipse. In this article, let us discuss how to find the foci of an ellipse in detail.

How to Find the Foci of an Ellipse?

Assume that “S” be the focus, and “l” be the directrix of an ellipse. Let Z be the foot of the perpendicular y’ from S on directrix l. Let A and A’ be the points which divide SZ in the ratio e:1. Let C is the midpoint of AA’ as the origin.

Let CA =a

⇒ A= (a,0) and A’=(-a,0).

Now (AS)/(AZ) = (e)/(1) = (A’S)/(A’Z)

⇒ SA = eAZ & SA’ = eA’Z

⇒ CA-CS = e(CZ-CA) ———>1

⇒ SC + CA’ = e(A’C+CZ) ———>2

Adding 1 and 2, we get

CA+CA’ = e(2CZ)

⇒ 2a = 2e*CZ

⇒ CZ = (a)/(e)

⇒ Equation of directrix is x = (a)/(e)

Subtracting 1 and 2, we get

2CS = e(2CA) = e*2a

⇒ CS =a

⇒ Focus, S= (ae,0)

Therefore, Foci = (ae, 0) & (-ae, 0) due to the symmetry.

Let us consider that P(x,y) be the point on ellipse and PM be the perpendicular distance from P to l

By the definition of Ellipse,

(SP)/(PM) =e

⇒SP = e PM

⇒SP² = e² PM²

(x-ae)² + y² = e²[ (x²+a²)/(e²) – (2ax)/(e) ]

x²/a² + (y²)/(a²(1-e²)) =1

e<1, 1-e² > 0

⇒ a²(1-e²) >0

Let it be b²

Then,

(x²/a²) + (y²/b²) = 1

Which is the equation of an ellipse.

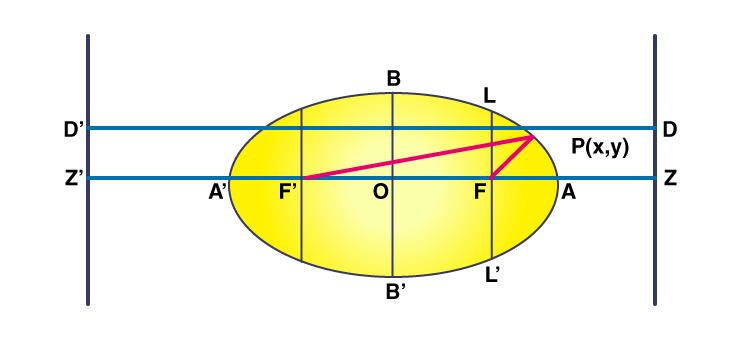
Focus-Directrix Property of an Ellipse

Consider an ellipse (x²/a²)+(y²/b²) = 1 .

Draw the lines ZD and ZD’ whose equations are x = a/e and x = -a/e respectively

Let P(x,y) be any two points on the ellipse. Let D’ PD be parallel to the x-axis.

The foci are F(c,o) and F’ (-c,o).

Now PF+PF’ =2a (by definition of an ellipse)

√[(x-c)²+y²]+√[(x+c)²+y²] = 2a

√[(x+c)²+y²] = 2a – √[(x-c)²+y²]

(x+c)²+y² =4a² + (x-c)²+y² -4a√[(x-c)²+y²]

√[(x-c)²+y²] = [a-(c/a)x]

PF= a-(c/a)x

PF = e[(a/e) – (c/de)x ] where c=ae

PF = e[(a/e)-x]

PF = e . PD ——– (1)

Further PF+PF’ = 2a

PF’ = 2a – PF

2a-a+ex = a+ex = e[(a/e)+x]

a+ex = e[(a/e)+x] = e PD’ ——– (2)

From (1) and (2) we have PF/PD = e and PF’ /PD’ = e

This shows that an ellipse is the locus of a point that moves in such a way that the ratio of its distance from a focus called fixed point to its distance from a directrix called fixed line equals a constant e<1.

Notes:

For the ellipse (x²/a²)+(y²/b²) = 1 ,we have:

• centre O (0, 0)
• Vertices A(a, 0) and A’(-a, 0)
• Major axis axis =2a and minor axis = 2b
• eccentricity e = √1-(b²/a²)
• The foci are F (ae, 0) and F’(-ae, 0)
• The equation of the directrix are x = a/e and x = -a/e

Foci of an Ellipse Example

Question:

Find the coordinate points of foci for the following ellipse: x² + 2y² = 3

Solution:

Given:

Ellipse equation: x² + 2y² = 3

The given equation can be written as:

x²/3 + y²/(3/2) = 1

Therefore, a = √3 and b = √(3/2) where a >b

Therefore, b² = a² (1-e²)

e = 1/ √2

Foci = (+ae,0) and (-ae,0)

Therefore, the coordinates of the foci are: (√(3/2), 0) and (√(-3/2), 0)

Stay tuned with BYJU’S – The Learning App to study all the important Maths-related articles to learn with ease.