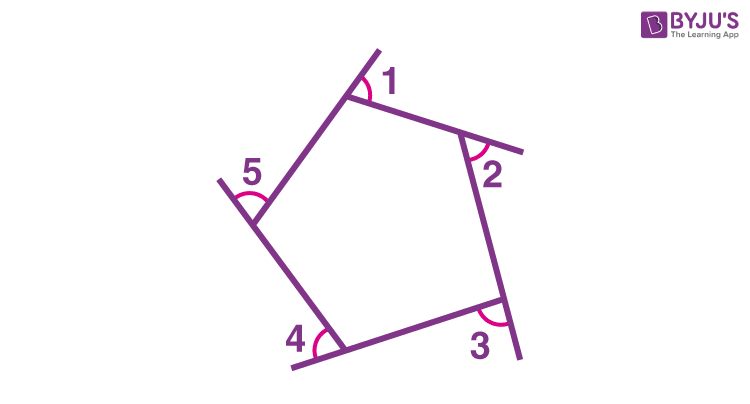
Interior Angles of a Polygon
Interior Angles of A Polygon: In Mathematics, an angle is defined as the figure formed by joining the two rays at the common endpoint. An interior angle is an angle inside a shape. The polygons are the closed shape that has sides and vertices. A regular polygon has all its interior angles equal to each other. For example, a square has all its interior angles equal to the right angle or 90 degrees.
The interior angles of a polygon are equal to a number of sides. Angles are generally measured using degrees or radians. So, if a polygon has 4 sides, then it has four angles as well. Also, the sum of interior angles of different polygons is different.
| Table of Contents: |
What is Meant by Interior Angles of a Polygon?
An interior angle of a polygon is an angle formed inside the two adjacent sides of a polygon. Or, we can say that the angle measures at the interior part of a polygon are called the interior angle of a polygon. We know that the polygon can be classified into two different types, namely:
- Regular Polygon
- Irregular Polygon
For a regular polygon, all the interior angles are of the same measure. But for irregular polygon, each interior angle may have different measurements.
Sum of Interior Angles of a Polygon
The Sum of interior angles of a polygon is always a constant value. If the polygon is regular or irregular, the sum of its interior angles remains the same. Therefore, the sum of the interior angles of the polygon is given by the formula:
Sum of the Interior Angles of a Polygon = 180 (n-2) degrees
As we know, there are different types of polygons. Therefore, the number of interior angles and the respective sum of angles is given below in the table.
| Polygon Name | Number of Interior Angles | Sum of Interior Angles = (n-2) x 180° |
| Triangle | 3 | 180° |
| Quadrilateral | 4 | 360° |
| Pentagon | 5 | 540° |
| Hexagon | 6 | 720° |
| Septagon | 7 | 900° |
| Octagon | 8 | 1080° |
| Nonagon | 9 | 1260° |
| Decagon | 10 | 1440° |
Interior angles of Triangles
A triangle is a polygon that has three sides and three angles. Since, we know, there is a total of three types of triangles based on sides and angles. But the angle of the sum of all the types of interior angles is always equal to 180 degrees. For a regular triangle, each interior angle will be equal to:
180/3 = 60 degrees
60°+60°+60° = 180°
Therefore, no matter if the triangle is an acute triangle or obtuse triangle or a right triangle, the sum of all its interior angles will always be 180 degrees.
Interior Angles of Quadrilaterals
In geometry, we have come across different types of quadrilaterals, such as:
- Square
- Rectangle
- Parallelogram
- Rhombus
- Trapezium
- Kite
All the shapes listed above have four sides and four angles. The common property for all the above four-sided shapes is the sum of interior angles is always equal to 360 degrees. For a regular quadrilateral such as square, each interior angle will be equal to:
360/4 = 90 degrees.
90° + 90° + 90° + 90° = 360°
Since each quadrilateral is made up of two triangles, therefore the sum of interior angles of two triangles is equal to 360 degrees and hence for the quadrilateral.
Interior angles of Pentagon
In case of the pentagon, it has five sides and also it can be formed by joining three triangles side by side. Thus, if one triangle has sum of angles equal to 180 degrees, therefore, the sum of angles of three triangles will be:
3 x 180 = 540 degrees
Thus, the angle sum of the pentagon is 540 degrees.
For a regular pentagon, each angle will be equal to:
540°/5 = 108°
108°+108°+108°+108°+108° = 540°
| Sum of Interior angles of a Polygon = (Number of triangles formed in the polygon) x 180° |
Interior angles of Regular Polygons
A regular polygon has all its angles equal in measure.
| Regular Polygon Name | Each interior angle |
| Triangle | 60° |
| Quadrilateral | 90° |
| Pentagon | 108° |
| Hexagon | 120° |
| Septagon | 128.57° |
| Octagon | 135° |
| Nonagon | 140° |
| Decagon | 144° |
Interior Angle Formulas
The interior angles of a polygon always lie inside the polygon. The formula can be obtained in three ways. Let us discuss the three different formulas in detail.
Method 1:
If “n” is the number of sides of a polygon, then the formula is given below:
Interior angles of a Regular Polygon = [180°(n) – 360°] / n
Method 2:
If the exterior angle of a polygon is given, then the formula to find the interior angle is
Interior Angle of a polygon = 180° – Exterior angle of a polygon
Method 3:
If we know the sum of all the interior angles of a regular polygon, we can obtain the interior angle by dividing the sum by the number of sides.
Interior Angle = Sum of the interior angles of a polygon / n
Where
“n” is the number of polygon sides.
Interior Angles Theorem
Below is the proof for the polygon interior angle sum theorem
Statement:
In a polygon of ‘n’ sides, the sum of the interior angles is equal to (2n – 4) × 90°.
To prove:
The sum of the interior angles = (2n – 4) right angles
Proof:
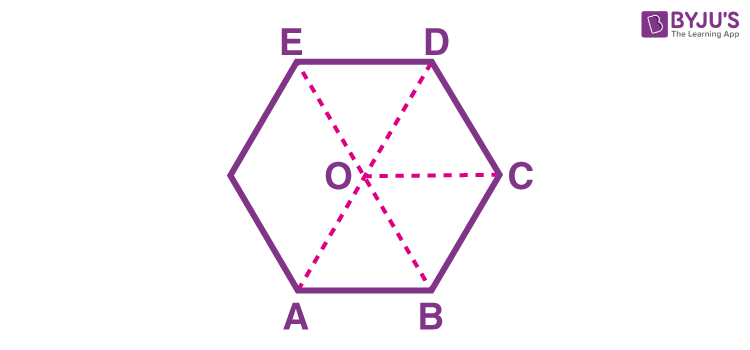
ABCDE is a “n” sided polygon. Take any point O inside the polygon. Join OA, OB, OC.
For “n” sided polygon, the polygon forms “n” triangles.
We know that the sum of the angles of a triangle is equal to 180 degrees
Therefore, the sum of the angles of n triangles = n × 180°
From the above statement, we can say that
Sum of interior angles + Sum of the angles at O = 2n × 90° ——(1)
But, the sum of the angles at O = 360°
Substitute the above value in (1), we get
Sum of interior angles + 360°= 2n × 90°
So, the sum of the interior angles = (2n × 90°) – 360°
Take 90 as common, then it becomes
The sum of the interior angles = (2n – 4) × 90°
Therefore, the sum of “n” interior angles is (2n – 4) × 90°
So, each interior angle of a regular polygon is [(2n – 4) × 90°] / n
Note: In a regular polygon, all the interior angles are of the same measure.
Exterior Angles
Exterior angles of a polygon are the angles at the vertices of the polygon, that lie outside the shape. The angles are formed by one side of the polygon and extension of the other side. The sum of an adjacent interior angle and exterior angle for any polygon is equal to 180 degrees since they form a linear pair. Also, the sum of exterior angles of a polygon is always equal to 360 degrees.
| Exterior angle of a polygon = 360 ÷ number of sides |
Related Articles
Solved Examples
Q.1: If each interior angle is equal to 144°, then how many sides does a regular polygon have?
Solution:
Given: Each interior angle = 144°
We know that,
Interior angle + Exterior angle = 180°
Exterior angle = 180°-144°
Therefore, the exterior angle is 36°
The formula to find the number of sides of a regular polygon is as follows:
Number of Sides of a Regular Polygon = 360° / Magnitude of each exterior angle
Therefore, the number of sides = 360° / 36° = 10 sides
Hence, the polygon has 10 sides.
Q.2: What is the value of the interior angle of a regular octagon?
Solution: A regular octagon has eight sides and eight angles.
n = 8
Since, we know that, the sum of interior angles of octagon, is;
Sum = (8-2) x 180° = 6 x 180° = 1080°
A regular octagon has all its interior angles equal in measure.
Therefore, measure of each interior angle = 1080°/8 = 135°.
Q.3: What is the sum of interior angles of a 10-sided polygon?
Answer: Given,
Number of sides, n = 10
Sum of interior angles = (10 – 2) x 180° = 8 x 180° = 1440°.
Practise Questions
- Find the number of sides of a polygon, if each angle is equal to 135 degrees.
- What is the sum of interior angles of a nonagon?
Register with BYJU’S – The Learning App and also download the app to learn with ease.
Frequently Asked Questions – FAQs
What are the interior angles of a polygon?
What is the formula to find the sum of interior angles of a polygon?
Sum = (n-2) x 180°
Where n is the number of sides or number of angles of polygons.
How to find the sum of interior angles by the angle sum property of the triangle?
4 x 180° = 720 degrees.
What is the measure of each angle of a regular decagon?
Sum of interior angles = (10 – 2) x 180°
= 8 × 180°
= 1440°
A regular decagon has all its interior angles equal in measure. Therefore,
Each interior angle of decagon = 1440°/10 = 144°