Prime Factors
Definition of a Factor
Factors are numbers that can be multiplied together to get another number. This also means that the division of a number with all the factors will result in 0 remainders. In simple words, we can say that a factor of a particular is an exact divisor of that number.
Let’s tackle this topic, prime factors one by one. A factor is generally described in the dictionary as a circumstance, event or action that contributes to the result. So you see, the factor is something that affects the outcome. In mathematics, it plays quite a similar role. Factors happen to be numbers that multiply to create another number.
For instance, take 3 * 2 = 6. Here 3 and 2 are factors of 6.
Prime Number-A number that has only two factors i.e. 1 and the number itself is known as Prime Number.
What are Prime Factors?
The factors of a number that are prime numbers are called prime factors of that number. As we know, 2 and 4 are the factors of 4, where 4 is considered as the prime factor of 4.
How to check whether the number is Prime or not?
The following two methods will help you to find whether the given number is a prime or not.
Method 1:
We know that 2 is the only even prime number. And only two consecutive natural numbers which are prime are 2 and 3. Apart from those, every prime number can be written in the form of 6n + 1 or 6n – 1 (except the multiples of prime numbers, i.e. 2, 3, 5, 7, 11), where n is a natural number.
For example:
6(1) – 1 = 5
6(1) + 1 = 7
6(2) – 1 = 11
6(2) + 1 = 13
6(3) – 1 = 17
6(3) + 1 = 19
6(4) – 1 = 23
6(4) + 1 = 25 (multiple of 5)
…
Method 2:
To know the prime numbers greater than 40, the below formula can be used.
n2 + n + 41, where n = 0, 1, 2, ….., 39
For example:
(0)2 + 0 + 0 = 41
(1)2 + 1 + 41 = 43
(2)2 + 2 + 41 = 47
…..
Prime Factors List
The prime factors of numbers up to 100 are given in the table below:
| Number | Prime Factors | Number | Prime Factors | Number | Prime Factors |
| 2 | 2 | 35 | 5, 7 | 68 | 22.17, i.e. 2, 17 |
| 3 | 3 | 36 | 22.32, i.e. 2, 3 | 69 | 3, 23 |
| 4 | 22, i.e. 2 | 37 | 37 | 70 | 2, 5, 7 |
| 5 | 5 | 38 | 2, 19 | 71 | 71 |
| 6 | 2, 3 | 39 | 3,13 | 72 | 23.32, i.e. 2, 3 |
| 7 | 7 | 40 | 23.5, i.e 2, 5 | 73 | 73 |
| 8 | 23, i.e. 2 | 41 | 41 | 74 | 2, 37 |
| 9 | 32, i.e. 3 | 42 | 2, 3, 7 | 75 | 3.52, i.e. 3, 5 |
| 10 | 2, 5 | 43 | 43 | 76 | 22.19, i.e. 2, 19 |
| 11 | 11 | 44 | 22.11, i.e. 2, 11 | 77 | 7, 11 |
| 12 | 22.3, i.e. 2, 3 | 45 | 32.5, i.e. 3, 5 | 78 | 2, 3, 13 |
| 13 | 13 | 46 | 2, 23 | 79 | 79 |
| 14 | 2, 7 | 47 | 47 | 80 | 24.5, i.e. 2, 5 |
| 15 | 3, 5 | 48 | 24.3, i.e. 2, 3 | 81 | 34 |
| 16 | 24, i.e. 2 | 49 | 72, i.e. 7 | 82 | 2, 41 |
| 17 | 17 | 50 | 2.52, i.e. 2, 5 | 83 | 83 |
| 18 | 2.32, i.e. 2, 3 | 51 | 3, 17 | 84 | 22.3.7, i.e. 2, 3, 7 |
| 19 | 19 | 52 | 22.13, i.e. 2, 13 | 85 | 5, 17 |
| 20 | 22.5, i.e. 2, 5 | 53 | 53 | 86 | 2.43 |
| 21 | 3, 7 | 54 | 2.33, i.e. 2, 3 | 87 | 3, 29 |
| 22 | 2, 11 | 55 | 5, 11 | 88 | 23.11, i.e. 2, 11 |
| 23 | 23 | 56 | 23.7, i.e. 2, 7 | 89 | 89 |
| 24 | 23.3, i.e. 2, 3 | 57 | 3, 19 | 90 | 2.32.5, i.e. 2, 3, 5 |
| 25 | 52, i.e. 5 | 58 | 2, 29 | 91 | 7, 13 |
| 26 | 2, 13 | 59 | 59 | 92 | 22.23, i.e. 2, 23 |
| 27 | 33, i.e. 3 | 60 | 22.3.5, i.e. 2, 3, 5 | 93 | 3, 31 |
| 28 | 22.7, i.e. 2, 7 | 61 | 61 | 94 | 2, 47 |
| 29 | 29 | 62 | 2.31 | 95 | 5, 19 |
| 30 | 2, 3, 5 | 63 | 32.7, i.e. 3, 7 | 96 | 25.3, i.e. 2, 3 |
| 31 | 31 | 64 | 26, i.e. 2 | 97 | 97 |
| 32 | 25, i.e. 2 | 65 | 5, 13 | 98 | 2.72, i.e. 2, 7 |
| 33 | 3, 11 | 66 | 2, 3, 11 | 99 | 32.11, i.e. 3, 11 |
| 34 | 2, 17 | 67 | 67 | 100 | 22.52, i.e. 2, 5 |
How to Find Prime Factors of a Number?
There are two important methods of finding prime factors of a given number. They are:
- Prime Factors by Division Method
- Prime Factors using Factor Tree
Let’s learn how to find the prime factors of a number using these two methods along with examples here.
The below figure shows the prime factor of 1092 using the factor tree.

Prime Factorization
Any number can be written in the form of multiplication of their prime factors. This is known as Prime Factorization.
Prime factors can also be understood in terms of the factor tree. Imagine the number as the top of a tree and proceed by creating branches that represent different factors of it.
For example, take 90. It would be 2 * 45. Now take 45 that would be 5 * 9. Again 9 would be 3 * 3. Hence 90 is 2 * 3 * 3 * 5. So 90 end up being on the top, while 2, 3, 3 and 5 are the different branches of 45. And the branches end there since the numbers cannot be broken down further.
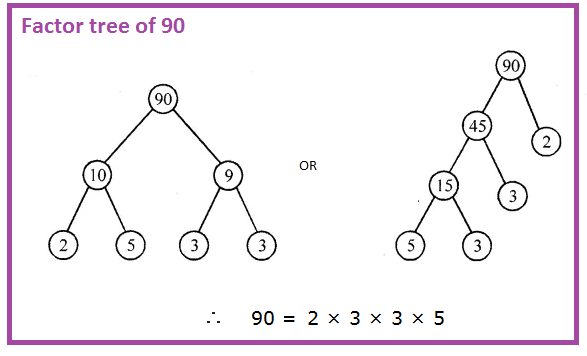
As shown in the above example, numbers can be categorized in various ways. You are already familiar with Whole numbers, decimal numbers, and fractions; but there are other special characteristics of numbers, which may be useful to consider as well. Numbers might be classified as even or odd, as perfect squares, as repeating or non-repeating decimals.
The other method to find the prime factors of a number apart from the factor tree is the short division method.
Let us find the prime factors of 60 using this method.
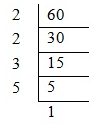
60 = 2 × 2 × 3 × 5
The short division method is also useful to find the Least Common Multiple of given numbers.
Solved Example
Example – Find all the prime factors of 627.
Solution- Creating a factor tree, we have;
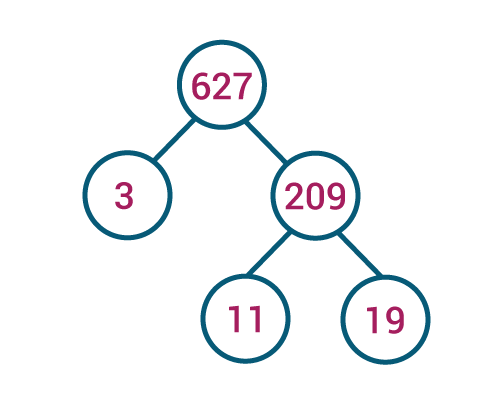
Thus 3,11,19 are the prime factors of 627.
i.e. 627 = 3 × 11 × 19.
Worksheet
- Write the prime factors of 36.
- What are the prime factors of 24?
- Find the prime factors of 72.
- How to calculate the prime factors of 5005 using the division method?
- Find the prime factors of 12 and 48 using the factor tree.
To better understand prime numbers and prime factorization download BYJU’S– The Learning App from Google Play Store and watch interactive videos.